LAB 5: ASSIGNMENT PROBLEMS AND SPARSE MATRICES
Mathematics:
The assignment problem is to assign tasks to facilities on a one-to-one basis in an optimal way. An example of the assignment problem is to assign n workers to n jobs such that the total cost (e.g. the costs of training, qualification-dependent salaries, etc.) is minimized. There are exactly n! = n*(n-1)*(n-2)*…*3*2*1 ways to assign n workers to n jobs. Costs of all n! combinations can be checked and the minimal cost can be found. However, such algorithm is computational inefficient, since the number of combinations grows fast with larger n, e.g. 10! = 3,628,800. Two Hungarian mathematicians, D. Konig and E. Egervary, proposed a better algorithm called the Hungarian method. This project exploits a simple computational method to approach to the optimal solution. (The Hungarian method would be the best solution but it is much more difficult to code).
Let us define the n-by-n cost matrix C and the n-by-n assignment matrix X:
C = 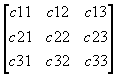 , X =
, X = 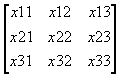
Here ci,j is
the cost of assigning the i-th worker to the j-th job
(in $) and xi,j is assignment, such that xi,j = 1 if
the i-th worker is assigned to the j-th job, and xi,j =
0, otherwise. The assignment is one-to-one if the matrix X has no two ones in the same row or in the same column. The cost of the current
assignment is
z = ![]()
![]() ci,j xi,j
ci,j xi,j
We will be working
with the following problem: assign n
= 9 candidates to n=9 jobs to minimize the total salary cost paid by the department. The
individual salaries of each candidate at each job position depend on their
qualification and are given by the cost matrix (in $ per hour):
|
|
Sam |
Jill |
John |
Liz |
Ann |
Lois |
Pete |
Alex |
Herb |
|
Administrator |
20 |
15 |
10 |
10 |
17 |
23 |
25 |
5 |
15 |
|
Secretary to the
Chair |
10 |
10 |
12 |
15 |
9 |
7 |
8 |
7 |
8 |
|
Undergraduate
Secretary |
12 |
9 |
9 |
10 |
10 |
5 |
7 |
13 |
9 |
|
Graduate
Secretary |
13 |
14 |
10 |
15 |
15 |
5 |
8 |
20 |
10 |
|
Financial Clerk |
12 |
13 |
10 |
15 |
14 |
5 |
9 |
20 |
10 |
|
Secretary |
15 |
14 |
15 |
16 |
15 |
5 |
10 |
20 |
10 |
|
Web designer |
7 |
9 |
12 |
12 |
7 |
6 |
7 |
15 |
12 |
|
Receptionist |
5 |
6 |
8 |
8 |
5 |
4 |
5 |
10 |
7 |
|
Typist |
5 |
6 |
8 |
8 |
5 |
4 |
5 |
10 |
7 |
If we start with
the position of Administrator and assign it to Alex (he gets the minimal
salary for this position), then we assign the position of Secretary to Chair to Lois (he gets the minimal
salary for this position), and so on, up to the position of Typist, then the assignment is given by the assignment matrix:
X =
0 0 0 0
0 0 0 1 0
0 0
0 0 0 1 0
0 0
0 0
0 0 0 0 1
0 0
0
0 1 0 0 0
0 0 0
0 0
0 0 0 0 0
0 1
0 1
0 0 0 0 0
0 0
1 0
0 0 0 0 0
0 0
0 0
0 0 1 0
0 0 0
0 0
0 1 0 0 0
0 0
where the total
cost z = 73. The optimal assignment is however different
from the first-to-assign solution above. The optimal assignment is:
X = 0 0
0 0 0 0
0 1 0
0 0
0 0 0 0 0
0 1
0 0
0 1 0 0 0
0 0
0 0
0 0 0 0 1
0 0
0 0
1 0 0 0 0
0 0
0 0
0 0 0 1 0
0 0
0 0
0 0 1 0 0
0 0
1 0
0 0 0 0 0
0 0
0 1
0 0 0 0 0
0 0
where the total
minimal cost z* =
64.
Objectives:
·
understand
computational algorithms for solving the assignment problems
·
code
the computational algorithms by using MATLAB programming constructions
·
exploit
the algorithms for different assignment problems
MATLAB script for solving the assignment problem by checking costs of all possible assignments
Steps
of the computational algorithm:
- Input the cost matrix C
and
find the size of the matrix.
- Construct all possible permutations of n numbers (n! combinations). Use function "perms" to build a n!-by-n matrix
of permutations.
- For each row of the
permutation matrix:
a)
Build
up the assignment matrix X from a zero n-by-n matrix
by assigning 1 row-by-row to the columns of the permutation
matrix.
b)
Compute the total cost z of
the assignment. Use
function "sum" to compute z.
- Find the assignment
with the minimal cost and display the cost z* and
the assignment matrix X.
MATLAB script for solving the assignment problem by approaching to the optimal solution
Steps
of the computational algorithm:
- Build up the assignment
matrix X from a zero n-by-n matrix by
assigning 1 row-by-row to the column, where the cost is
minimal compared to costs in other columns of the given row. If the
minimal cost occurs in the column that has already the 1-assigned
position in the rows above the given row, take the
column with the second minimal cost, and so on.
a)
Organize
a single loop for rows of matrix X.
b)
Use
MATLAB function "sort" with two output arguments (for the
value and for its index in the row) to sort costs in the ascending order.
c)
Organize
another loop for elements of the sorted vector in the ascending order.
d)
Use
MATLAB function "any" to check if the selected column has
already non-zero values.
- Consider two 1-assigned
positions at (i1,j1) and (i2,j2).
This assignment has the cost: ci1,j1 + ci2,j2.
If the workers would interchange with their jobs, the new cost
would be: ci1,j2 + ci2,j1. After the
interchange, he new assignment is more optimal if the difference in costs
is negative, i.e. Dz = ci1,j2 + ci2,j1 - ci1,j1
- ci2,j2 < 0.
- Starting with the given
assignment matrix X, loop through all rows of X making
exchange of 1-assigned positions, if necessary.
e)
For
each row, compute the difference in costs that would result if the current 1-assigned
position interchanges with the position in the other (n-1)
column. You should compute (n-1) numbers for each row.
f)
Use
functions "find" and "min".
g)
If
all numbers are positive or zero, move to the next row.
h)
If
there exists a negative value for Dz, select the minimal value of
Dz and make the interchange of 1-s and 0-s in
the corresponding positions in the assignment matrix X.
i)
Compute
the total cost of the new assignment.
- If there were negative
entries Dz in step (2), proceed with step (4) again. If all
entries Dz were positive or zero, stop the algorithm and
compute the total minimal cost z of the found assignment
matrix X.
- The computational
algorithm will stop in a finite number of iterations, where the minimal
cost solution is reached. However, your solution may not be optimal yet,
but very close to the optimal solution. In general algorithm, step (3) has
to be modified since more complicated exchanges of assignments (involving
three and more interchanges at the same time) may still result in the
decrease of the total cost. Compare the minimal cost solution obtained in
the second script with the optimal solution obtained in the first script
in this laboratory.
Quiz:
- Modify the scripts by
using the function "sparse" for sparse assignment matrix X.
- Find the optimal
assignment for the following cost matrices:
(a)  (b)
(b) 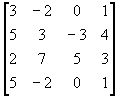 (c)
(c) 