CHAPTER 4: MATHEMATICAL MODELING WITH MATLAB

 

Lecture 4.1: Finite difference approximations for numerical derivatives

 

Forward, backward, and central differences for derivatives:

 

Problem: Given a set of data points near the point (x0,y0):

…; (x-2,y-2); (x-1,y-1); (x0,y0); (x1,y1); (x2,y2); …

Suppose the data values represent values of a function y = f(x). Find a numerical approximation for derivatives f'(x0), f''(x0), … of the function y = f(x) at the point (x0,y0).

 


Example: Linear electrical circuits consist of resistors, capacitors, inductors, and voltage and current sources. In a simple resistor-inductor (RL) one-port network driven by a current source, the voltage V = V(t) develops across the port terminals when a current I = I(t) is applied to the input port, The voltage output V(t) can be determined as a sum of the voltage drop across the resistor R I(t) and of the voltage drop across the inductor L I'(t). The derivative I'(t) is to be found from the input current I(t) measured at different time instances:

 


Solution: The first derivative f'(x0) of the function y = f(x) at the point (x0,y0) can be approximated by the slope of the secant line that passes through two points (linear piecewise interpolation). Depending on whether the points are taken to the right of the point (x0,y0)  (future data), to the left of the point (x0,y0) (past data), or to both sides, the slope of the secant line is called the forward, backward or central difference approximations.

 

Forward difference approximation:

 

The secant line passes the points (x0,y0) and (x1,y1).

                f'(x0)  Dforward(f;x0) =

Forward differences are useful in solving initial-value problems for differential equations by single-step predictor-corrector methods (such as Euler methods). Given the values f'(x0) and f(x0), the forward difference approximates the value f(x1).

Backward difference approximation:

 

The secant line passes the points (x-1,y-1) and (x0,y0).

            f'(x0)  Dbackward(f;x0) =

Backward differences are useful for approximating the derivatives if the data values are available in the past but not in the future (such as secant methods for root finding and control problems). Given the values f(x-1) and f(x0), the backward difference approximates the value f(x1), if it depends on f'(x0).

Central difference approximation:

 

The secant line passes the points (x-1,y-1) and (x1,y1).

             f'(x0)  Dcentral(f;x0) =

Central differences are useful in solving boundary-value problems for differential equations by finite difference methods. Approximating values of f'(x0) that occurs in differential equations or boundary conditions, the central difference relates unknown values f(x-1)  and f(x1) by an linear algebraic equation.

h  = 0.1; x0 = 1; x_1 = x0-h; x1 = x0 + h;

% the three data points are located at equal distance h (the step size)

y0 = exp(10*x0); y_1 = exp(10*x_1); y1 = exp(10*x1); yDexact = 10*exp(10*x0);

yDforward = (y1-y0)/h; % simple form of forward difference for equally spaced grid

yDbackward = (y0-y_1)/h;  % simple form of backward difference

yDcentral = (y1-y_1)/(2*h);  % simple form of central difference

fprintf('Exact = %6.2f\nForward = %6.2f\nBackward = %6.2f\nCentral = %6.2f',yDexact,yDforward,yDbackward,yDcentral);  

Exact = 220264.66

Forward = 378476.76

Backward = 139233.82

Central = 258855.29  

 

Errors of numerical differentiation:

 

Numerical differentiation is inherently ill-conditioned process. Two factors determine errors induced when the derivative f'(x0) is replaced by a difference approximations: truncation and rounding errors.

 

Consider the equally spaced data points with constant step size: h = x1 – x0 = x0 –  x-1. The theory based on the Taylor expansion method shows the following truncation errors:

·         Forward difference approximation:

f'(x0) – Dforward(f,x0) = -f''(x),    x  [x0,x1]

The truncation error of the forward difference approximation is proportional to h, i.e. it has the order of O(h). The error is also proportional to the second derivative of the function f(x) at an interior point x of the forward difference interval.

 

·         Backward difference approximation:

f'(x0) – Dbackward(f,x0) =  f''(x),    x  [x-1,x0]

The truncation error of the backward difference approximation is as bad as that of the forward difference approximation. It also has the order of O(h) and is also proportional to the second derivative of the function f(x) at an interior point x of the backward difference interval.

·         Central difference approximation:

f'(x0) – Dcentral(f,x0) = -f'''(x),    x  [x-1,x1]

The truncation error of the central difference approximation is proportional to h2 rather than h, i.e. it has the order of O(h2). The error is also proportional to the third derivative of the function f(x) at an interior point x of the central difference interval. The central difference approximation is an average of the forward and backward differences. It produces a much more accurate approximation of the derivative at a given small value of h, compared to the forward and backward differences. If the data values are available both to the right and to the left of the point (x0,y0), the use of the central difference approximation is the most preferable.

h = logspace(-1,-16,16);

x0 = 1; x_1 = x0-h; x1 = x0+h;

y0 = exp(10*x0); y_1 = exp(10*x_1); y1 = exp(10*x1); yDe = 10*exp(10*x0);

yDf = (y1-y0)./h; yDb = (y0-y_1)./h;  yDc = (y1-y_1)./(2*h); 

eDf = abs(yDf-yDe); eDb = abs(yDb-yDe); eDc = abs(yDc-yDe);

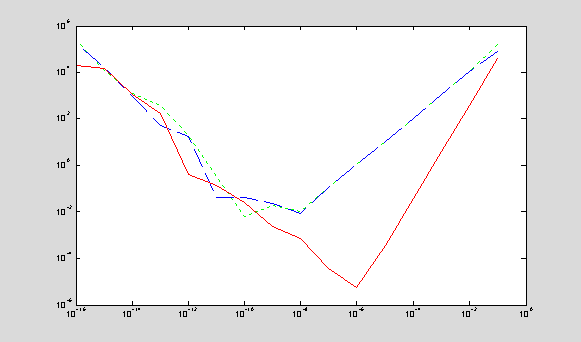
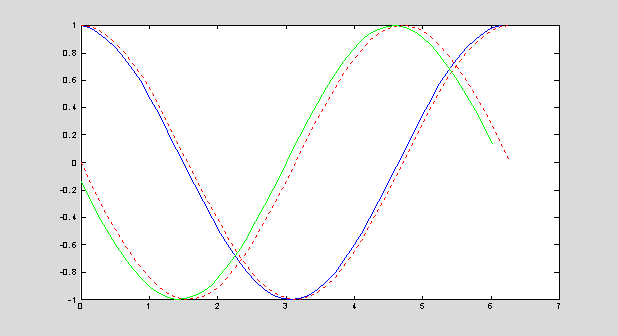
loglog(h,eDf,'g:',h,eDb,'b--',h,eDc,'r');  

 

  

 

If the step size h between two points becomes smaller, the truncation error of the difference approximation decreases. It decreases faster for central difference approximations and slower for forward and backward difference approximations. For example, if h is reduced by a factor of 10, the truncation error of the central difference approximation is reduced by a factor of 100, while the truncation errors of the forward and backward differences are reduced only by a factor of 10.

 

When h becomes too small, the difference approximations are taken for almost equal values of f(x) at the two points. Any rounding error of computations of f(x) is magnified by a factor of 1/h. As a result, the rounding error grows with h for very small values of h. An optimal step size h = hopt can be computed from minimization of the sum of truncation and rounding errors:

 

·         Forward difference approximation:

eforward = | f'(x0) – Dforward(f,x0)| <  M2  + 2 ,

where M2 = max | f''(x)|. The minimum of error occurs for h = hopt =2, when eforward = 2.

·         Central difference approximation:

ecentral = | f'(x0) – Dcentral(f,x0)| < M3 + 2 ,

where M3 = max | f'''(x)|. The minimum of error occurs for h = hopt =, when eforward = 3.

 

M2 = 100*exp(10*(x0+0.1));

M3 = 1000*exp(10*(x0+0.1));

hoptForward = 2*(eps/M2)^(1/2)

hoptCentral = (6*eps/M3)^(1/3)

eoptForward = 2*(eps*M2)^(1/2)

eoptCentral = 3*(eps^2*M3/6)^(1/3)  

 

hoptForward =  1.2180e-011

hoptCentral =  2.8127e-008

eoptForward =  7.2924e-005

eoptCentral =  2.3683e-008  

 

 

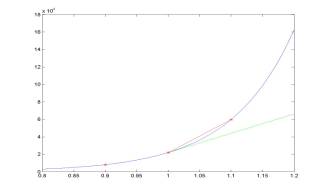
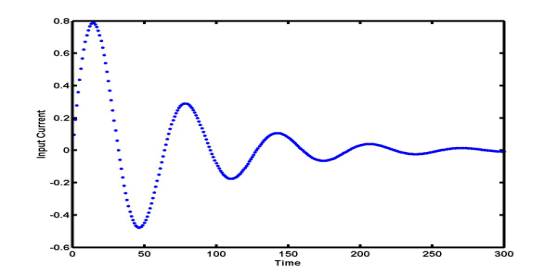
Example: Two central difference approximations are applied to compute the derivative of the current I'(t): green pluses are for h = 10 and blue dots are for h = 5. The exact derivative I'(t) is shown by red solid curve.

 

 

Newton forward difference interpolation:

 

Problem: Given a set of (n+1) data points:

(x1,y1); (x2,y2); …; (xn,yn); (xn+1,yn+1)

 

Find a Newton polynomial of degree n, y = Pn(x),  that passes through all (n+1) data points. The Newton polynomial is a discrete Taylor polynomial of the form:

 

y = Pn(x) = c0 + c1 (x-x1) + c2(x-x1)(x-x2) + cn (x – x1)(x – x2)…(x-xn)

where the coefficients cj are constructed from diagonal divided differences.

 

Comparison: Lagrange polynomial interpolation is convenient when the same grid points [x1,x2,…,xn+1]

are repeatevely used in several applications. The data values can be stored in computer memory to reduce a number. The Lagrange interpolation is not useful however when additional data points are added or removed to improve the appearance of the interpolating curve. The data set has to be completely recomputed every time when the data points are added or removed. The Newton polynomial interpolation is more convenient for adding and deleting additional data points. It is also more convenient for an algorithmic use of the Horner's nested multiplication. Of course, the Newton interpolating polynomials coincides with the Vandermond and Lagrange interpolating polynomials for a given data set, since the interpolating polynomial y = Pn(x) of order n connecting (n+1) data points are unique. The difference between Vandermonde, Lagrange, and Newton interpolating polynomials lies only in computational aspects.

 

Solution: The coefficients cj are to be found from the conditions: Pn(xk) = yk that results in a linear system:

Ac = y. The Gauss elimination algorithm or induction methods can be used to prove that cj = dj,j, where dj,j are diagonal entries in the table of forward divided differences:

 

grid

points

data

values

first

differences

second differences

third differences

fourth differences

x1

y1

 

 

 

 

x2

y2

f[x1,x2]

 

 

 

x3

y3

f[x2,x3]

f[x1,x2,x3]

 

 

x4

y4

f[x3,x4]

f[x2,x3,x4]

f[x1,x2,x3,x4]

 

x5

y5

f[x4,x5]

f[x3,x4,x5]

f[x2,x3,x4,x5]

f[x1,x2,x3,x4,x5]

 

Zero divided differences f[xk]  are simply the values of the function y = f(x) at the point (xk,yk). First divided differences f[xk,xk+1] are forward difference approximation for derivatives of the function y = f(x) at (xk,yk):

f[xk,xk+1] =

 

Second, third, and higher-order forward divided difference are constructed by using the recursive rule:

f[xk,xk+1,…,xk+m] =

 

With the use of divided differences cj-1 = f[x1,x2,…,xj], the Newton interpolating polynomial y = Pn(x) has the explicit representation:

Pn(x) = f[x1,x2,…,xj]

 

% example of explicit computation of coefficients of Newton polynomials

x = [ -1,-0.75,-0.5,-0.25,-0]; n = length(x)-1;

y = [ -14.58,-6.15,-1.82,-0.23,-0.00];

A = ones(n+1,1); % the coefficient matrix for linear system Ac = y

for j = 1 : n

A = [ A, A(:,j).*(x'-x(j))];

end

A, c = A\(y'); c = c'   

A = 1.0000         0         0         0         0

    1.0000    0.2500         0         0         0

    1.0000    0.5000    0.1250         0         0

    1.0000    0.7500    0.3750    0.0938         0

    1.0000    1.0000    0.7500    0.3750    0.0938

c =  -14.5800   33.7200  -32.8000   14.5067    0.2133  

 

function [yi,c] = NewtonInter(x,y,xi)

% Newton interpolation algorithm

% x,y - row-vectors of (n+1) data values (x,y)

% xi - a row-vector of x-values, where interpolation is to be found

% yi - a row-vector of interpolated y-values

% c - coefficients of Newton interpolating polynomial

n = length(x) - 1; % the degree of interpolation polynomial

ni = length(xi); % the number of x-values, where interpolation is to be found

D = zeros(n+1,n+1); % the matrix for Newton divided differences

D(:,1) = y'; % zero-order divided differences

for k = 1 : n

    D(k+1:n+1,k+1) = (D(k+1:n+1,k)-D(k:n,k))./(x(k+1:n+1)-x(1:n-k+1))';

end

c = diag(D);

% computation of values of the Newton interpolating polynomial at values of xi

% the algorithm uses the Horner's rule for polynomial evaluation

yi = c(n+1)*ones(1,ni); % initialization of the vector yi as the coefficient of the highest degree

for k = 1 : n

    yi = c(n+1-k)+yi.*(xi-x(n+1-k)); % nested multiplication

end  

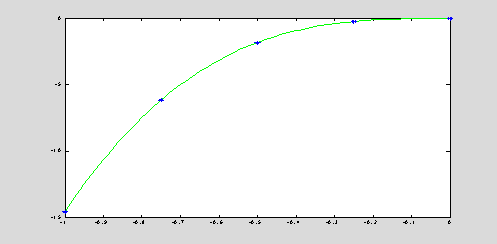
x = [ -1,-0.75,-0.5,-0.25,-0]; y = [ -14.58,-6.15,-1.82,-0.23,-0.00];

xInt = -1 : 0.01 : 0;

[yInt,c] = NewtonInter(x,y,xInt);

c = c', plot(xInt,yInt,'g',x,y,'b*');    

c =  -14.5800   33.7200  -32.8000   14.5067    0.2133

  

MATLAB finite differences:

 

Let the data points x1,x2,…,xn,xn+1 be equally spaced with constant step size h = x2 – x1. Then, the divided differences can be rewritten as:

f[xk,xk+1,…,xk+m] = ,

where  is the m-th forward difference of a function y = f(x) at the point (xk,yk).

 = y1 – y0

 = y2 – 2 y1 + y0

 = y3 –3 y2 + 3 y1 – y0

 = y4 – 4 y3 + 6 y2  -4 y1 – y0

 = y5 – 5 y4 + 10 y3 – 10 y2 + 5 y1 – y0

Derivatives of the interpolation polynomials y = Pn(x) approximate derivatives of the function y = f(x). Matching the n-th derivative of the polynomial y = Pn(x) with f(n)(x0), we find the forward difference approximation for higher-order derivatives:

f(n)(x0)

·         diff(y): computes first-order forward difference for a given vector y

·         diff(y,n): computes n-th order forward difference for a given vector y

·         gradient(u): computes horizontal and vertical forward differences for a given matrix to approximate the x- and y-derivatives of u(x,y): grad(u) = [ux,uy]

·         del2(u): computes a discrete Laplacian for a given matrix u: u = uxx + uyy

 

n = 50; x = linspace(0,2*pi,n); h = x(2)-x(1); y = sin(x); % function

y1 = diff(y)/h; y2 = diff(y,2)/h^2; y1ex = cos(x); y2ex = -sin(x);% derivatives

plot(x(1:n-1),y1,'b',x,y1ex,':r',x(1:n-2),y2,'g',x,y2ex,':r');   

 

Hierarchies of higher-order difference approximations:

 

Newton interpolating polynomials and divided difference tables can be constructed for backward differences, since the order of data points x1,x2,…,xn,xn+1 is arbitrary. By arranging for data points in descenting order, the Newton polynomial represents the backward differences. It is trickier to construct tables for central differences. Since central differences are the most accurate approximations, special algorithms are designed to automate derivation of coefficients of central difference approximations for higher-order derivatives.

 

·         hierarchy of forward differences:

Let the data points are equally spaced with constant step size h. Fix a point (x0,y0) and present a forward difference approximation for the n-th derivative as the inner product multiplication:

f(n)(x0) Dn*y

where y = [ y0,y1,y2, …]

n = 100; A = diag(ones(n-1,1),1)-diag(ones(n,1));

m = 8; B = A;

for k = 1 : m-1

D(k,:) = B(1,1:m);

B = B*A;

end

D = D  

D   -1     1     0     0     0     0     0     0

     1    -2     1     0     0     0     0     0

    -1     3    -3     1     0     0     0     0

     1    -4     6    -4     1     0     0     0

    -1     5   -10    10    -5     1     0     0

     1    -6    15   -20    15    -6     1     0

    -1     7   -21    35   -35    21    -7     1  

 

·         hierarchy of central differences

Let the data points are equally spaced with constant step size h. Fix a point (x0,y0) and present a central difference approximation for the n-th derivative as the inner product multiplication:

f(2m-1)(x0) D2m-1*y;         f(2m)(x0) D2m*y

where y = [ …,y-2,y-1,y0,y1,y2, …]

n = 100; A = diag(ones(n-1,1),1)-diag(ones(n-1,1),-1);

A2 = diag(ones(n-1,1),1)+diag(ones(n-1,1),-1)-2*diag(ones(n,1));

m = 4; B = A; C = A2; k = 1;

while (k < (2*m-2) )

D(k,:) = B(m,1:2*m-1);

D(k+1,:) = C(m,1:2*m-1);

B = B*A2; C = C*A2;

k = k+2;

end

D = D 

D =  0     0    -1     0     1     0     0

     0     0     1    -2     1     0     0

     0    -1     2     0    -2     1     0

     0     1    -4     6    -4     1     0

    -1     4    -5     0     5    -4     1

     1    -6    15   -20    15    -6     1  

 

 

Richardson extrapolation for higher-order differences:

 

Recursive difference formulas for derivatives can be obtained by canceling the truncation error at each order of numerical approximation. This method is called the Richardson extrapolation. It can be used only if the data values are equally spaced with constant step size h.

 

·         Recursive forward differences:

The hierarchy of forward differences for first and higher-order derivatives has the truncation error of order O(h). Denote the forward difference approximation for a derivative f(n)(x0) as D1(h). Compute the approximation with two step sizes h and 2h:

f(n)(x0) = D1(h) + h;     f(n)(x0) = D1(2h) + 2h

where  is unknown coefficient for the truncation error. By cancelling the truncation error of order O(h), we define a new forward difference approximation for the same derivative:

f(n)(x0) = 2D1(h) – D1(2h) = D2(h)

The new forward difference approximation D2(h) for the same derivative is more accurate since the truncation error is of order O(h2).

The first-order approximation D1(h) is a two-point divided difference, while the second-order approximation D2(h) is a three-point divided difference:

D1(h) = , D2(h) =

The first-order approximation D1(h) is a three-point divided difference, while the second-order approximation D2(h) is a four-point divided difference:

D1(h) = , D2(h) =

 

The process can be continued to find a higher-order forward-difference approximation Dm(h) with the truncation error O(hm). The recursive formula for Richardson forward difference extrapolation:

Dm+1(h) =Dm(h) +

·         Recursive central differences:

The hierarchy of central differences for first and higher-order derivatives has the truncation error of order O(h2). Denote the central difference approximation for a derivative f(n)(x0) as D1(h). Compute the approximation with two step sizes h and 2h:

f(n)(x0) = D1(h) + h2;     f(n)(x0) = D1(2h) + 4h2

where  is unknown coefficient for the truncation error. By cancelling the truncation error of order O(h2), we define a new central difference approximation for the same derivative:

f(n)(x0) =

The new central difference approximation D2(h) for the same derivative is more accurate since the truncation error is of order O(h4).

The first-order approximation D1(h) is a three-point divided difference, while the second-order approximation D2(h) is a five-point divided difference:

D1(h) = ,     D2(h) =

The first-order approximation D1(h) is a three-point divided difference, while the second-order approximation D2(h) is a five-point divided difference:

D1(h) = ,     D2(h) =

 

The process can be continued to find a higher-order central-difference approximation Dm(h) with the truncation error O(h2m). The recursive formula for Richardson forward difference extrapolation:

Dm+1(h) =Dm(h) +

·         Numerical algorithm

In order to compute the central difference approximation of a derivative f(n)(x0) up to order m, central difference approximations of lower order are to be computed with larger step sizes: h, 2h, 4h, 8h, …, (m-1)h.

These approximations can be arranged in a table of recursive derivatives:

step size

D1

D2

D3

D4

D5

h

D1(h)

 

 

 

 

2h

D1(2h)

D2(h)

 

 

 

4h

D1(4h)

D2(2h)

D3(h)

 

 

8h

D1(8h)

D2(4h)

D3(2h)

D4(h)

 

16h

D1(16h)

D2(8h)

D3(4h)

D4(2h)

D5(h)

The diagonal entries are values of higher-order central difference approximations for the derivative f(n)(x0)

where x0 is the central point surrounded by the points x = x0 - 2k-1h and x = x0 + 2k-1h for k = 1,2,…,m.

The higher-order approximation Dk(h) has the truncation error O(h2k). If h is small, the truncation error rapidly decreases with larger k. However, the rounding error grows with larger value of k. An optimal order m exists at the minimum of the sum of the truncation and rounding errors.

 

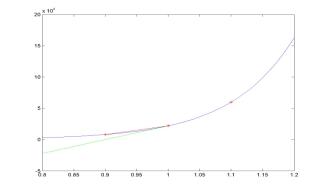
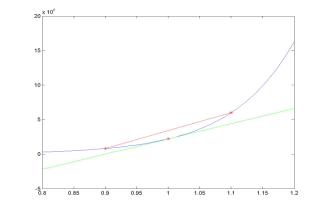
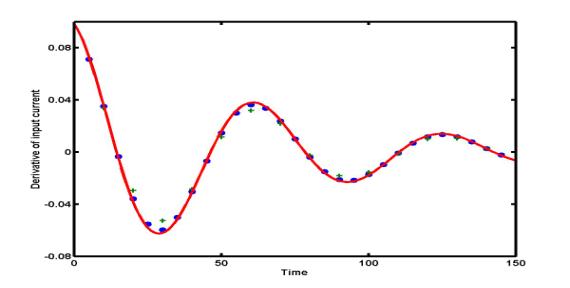
Example: The figure below presents the central difference approximations D1(h) and D2(h) for the derivative of the current I(t) with the step size h = 10. Blue circles are found by five-point central differences D2(h), green pluses are obtained by three-point central differences D1(h), and the exact derivative I'(t) is shown by a red solid curve. Five-point difference approximation D2(h) is clearly more accurate than the three-point difference D1(h).