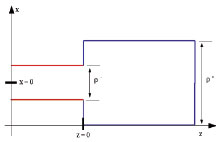
A material medium that confines and guides a propagating electromagnetic wave is referred to as a waveguide. The purpose of this project is to develop a computational algorithm for solving the stationary Maxwell equations at the interface between two planar waveguides, shown on figure.

The two-dimensional stationary Maxwell equations for the TE wave take the form of the Helmholtz equation:
Uxx + Uzz + k2 n2(x,z) U = 0,where k is the operating wavenumber, n(x,z) is the waveguide's refractive index, and U(x,z) is the amplitude of the TE electric field. Separating the variables x and z, we reduce the stationary problem to the two uncoupled eigenvalue problems:
Wxx + q+/-(x) W = λ W,where q+/- are defined for z>0 and z < 0, respectively, and λ is the eigenvalue. A typical spectrum of the eigenvalue problem is shown on the figure.

Matching the electric and magnetic fields on the interface z = 0, we derive linear system for amplitudes of spectral representations for U(x,z), solve it with the numerical linear algebra and graph the solution surface on the domain of (x,z). A typical solution surface is shown on these figures as a side plot and a top plot.
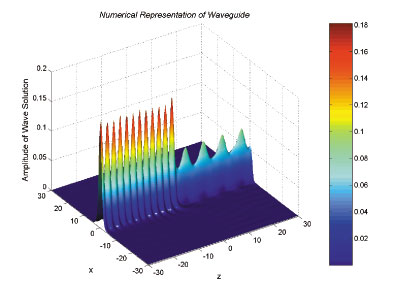
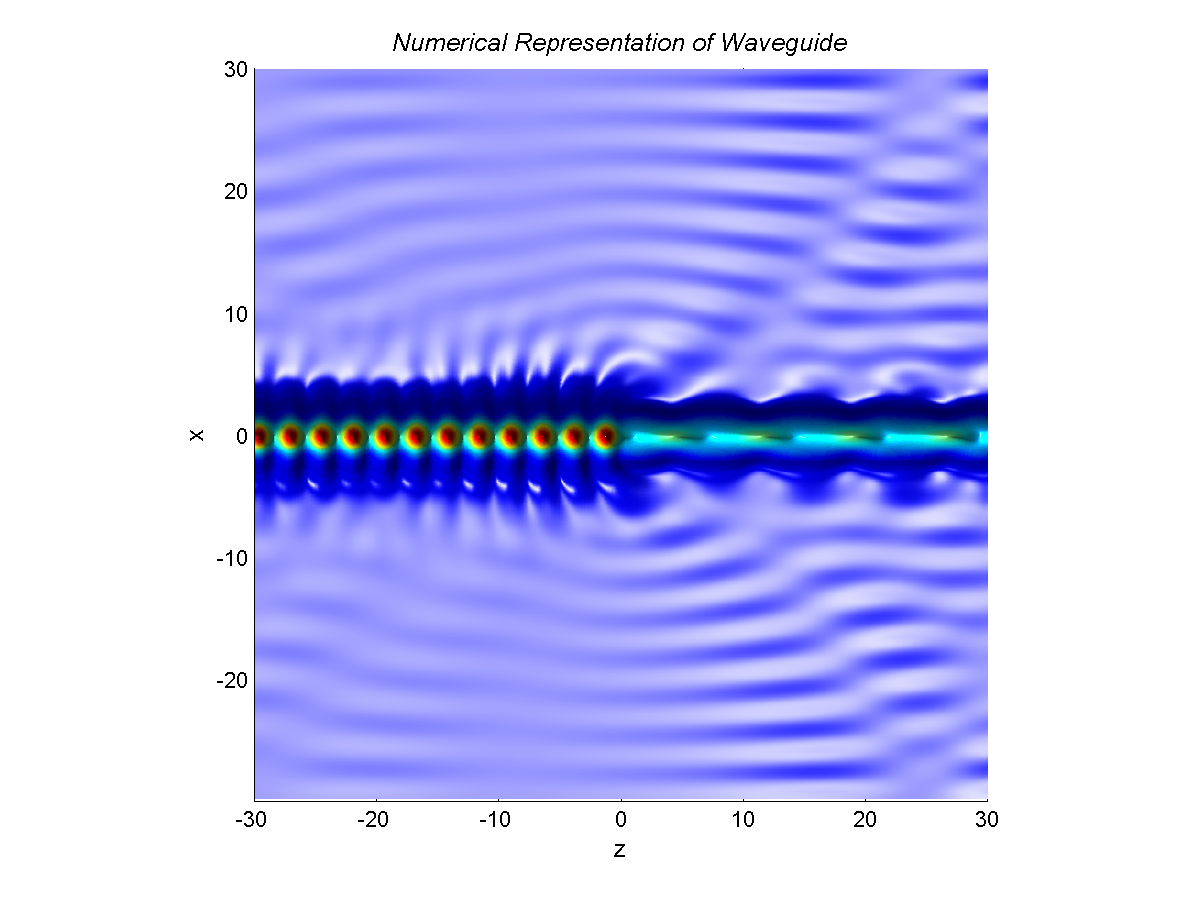
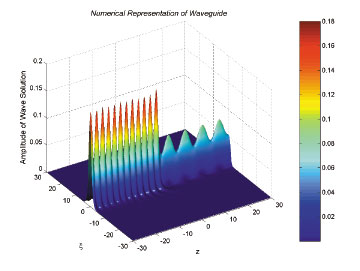
Numerical algorithm is modified with the absorbing layers, which absorb outgoing waves from arificial boundary-reflected waveguides. The solution surface with the absorbing layers is shown on the final figure.
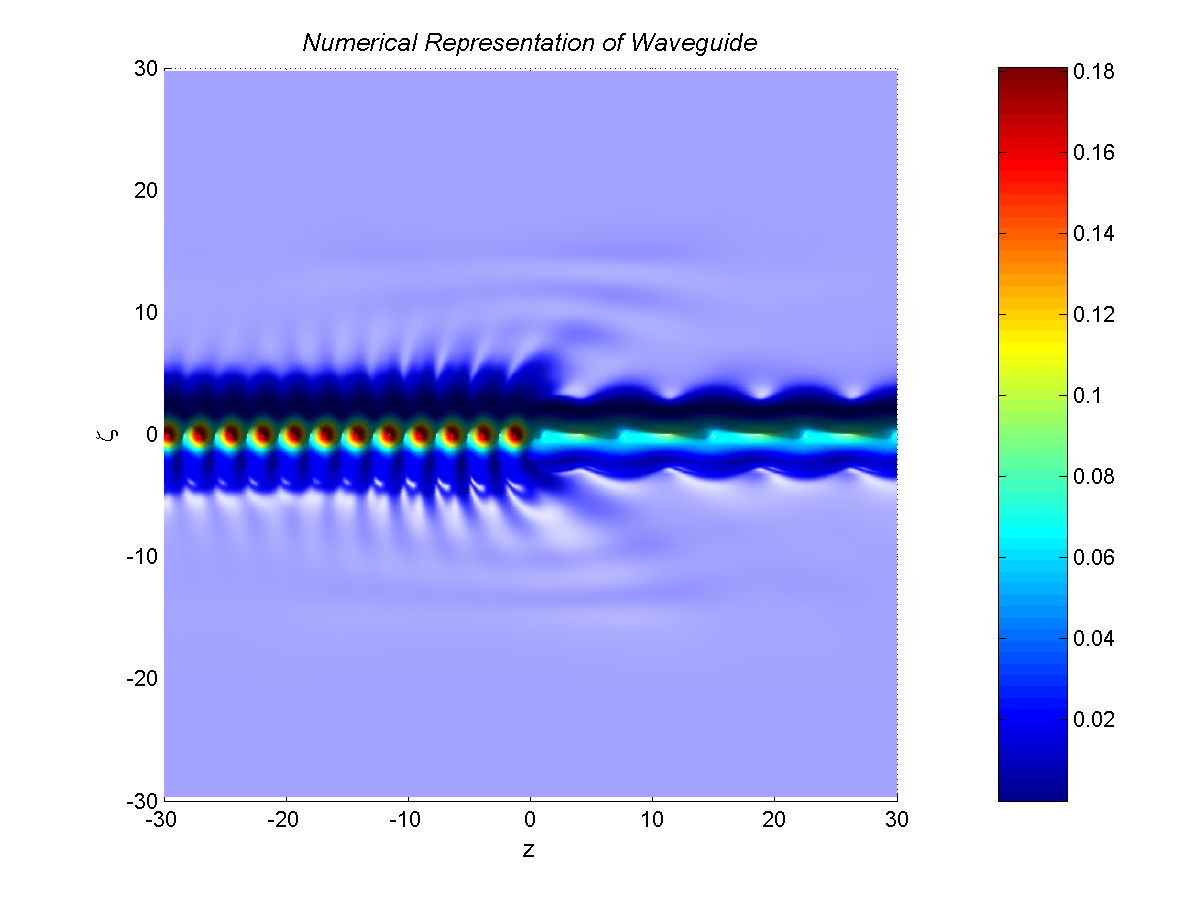
Besides computer visualizations of the solution surface, we also compute the energy spectrum for the reflected and transmitted modes. Most energy is trapped in the waveguide modes of the discrete spectrum, but there exist energy losses due to radiation and edge modes of the continuous spectrum. The sum of reflected and transmitted energies matches the incident energy due to the Poynting's theorem for the energy flux.

|
Run: Interactive software simulator |

|
Download MATLAB files: No absorbing layers With absorbing layers Energy spectrum |

|
Download: M.Sc. thesis of C. Webster |