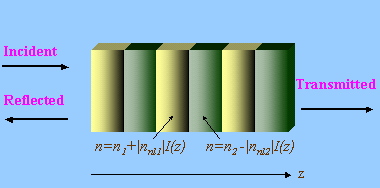
Optical limiters and switchers can be manufactured from alternating bulk layers of photonic crystals with different linear refractive indices and different Kerr nonlinearities. Transmission of light through the periodic material is simultaneously wavelength- and intensity-dependent. A typical heterogeneous nonlinear photonic crystals is shown below:

The stationary transmission of light signals through heterogeneous photonic crystals can be modelled with the coupled-mode nonlinear equations, derived near the first Bragg resonance in photonic band-gap spectrum:
i Ax + n0k B + nnl (|A|2 + 2 |B|2) A + n2k ((2|A|2 + |B|2) B + A2 B*) = 0,where A(x) is the amplitude of right-propagating wave, B(x) is the amplitude of left-propagating wave, n0k is the standard deviation of the linear refractive index, nnl is the average Kerr nonlinearity coefficient, and n2k is the standard deviation of the Kerr nonlinearity. The transmission problem of the coupled waves A(x) and B(x) is defined on the finite interval 0 < x < L, subject to the boundary conditions:
|A|2(0) = Iin, B(L) = 0.The transmitted intensity is defined as Iout = |A|2(L), while the reflected intensity is Iref = |B|2(0) = Iin - Iout. The curve Iout versus Iin is called the input-output transmission characteristics. There are two typical input-output characteristics for heterogeneous photonic crystals, shown on the figure:
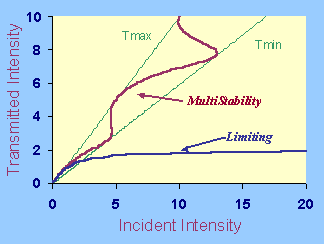
In the interactive software, the input-output transmission characteristics are computed versus the three parameters of the coupled-mode equations n0k, nnl, and n2k, the length of the heterogeneous photonic crystal L, and the range of the interval for transmitted intensity Istart < Iout < Ifin. The results are displayed in a single graph.

|
Run: Interactive software simulator |

|
Download MATLAB files: Stationary problem Linearization spectrum Time-dependent problem Pulse transmission |

|
Download: JOSA B papers: I, II, III M.Sc. thesis of D. Agueev |