
Linear dispersive waves propagate according to their dispersion relation, which is a relation between the wavevector k and frequency ω so that ω = ω(k). In linear systems, waves of different wavevectors and frequencies do not interact due to the Linear Superposition Principle. In nonlinear systems, the lowest-order nonlinear effect (expanding in the wave amplitudes) is the resonant interaction between N waves of different wavevectors kj and frequencies ωj which satisfy the resonance conditions:
∑j=1N kj = 0, ∑j=1N ω(kj) = 0.The simplest three-wave resonant interaction occurs if there are non-trivial solutions of the system: k = k1 + k2 and ω(k) = ω(k1) + ω(k2). Resonant wave configurations are defined entirely by the dispersion relation ω = ω(k). Some dispersion relations do not exhibit non-trivial solutions of the resonance conditions for any k1 and k2. Some others may exhibit resonant three-wave interactions, e.g. the deep-water gravity-capillary waves satisfying the dispersion relation ω(k) = g |k| + T |k|3, where g is gravity accelaration and T is the surface tension coefficient. When T is non-zero, the resonant configurations of the three waves occur already in one space dimension, as shown on the graphical solution.

When T = 0, the resonant three-wave configurations do not occur in space of any dimensions, but the deep-water gravity waves satisfying the dispersion relation ω2 = g|k| exhibit the resonant four-wave interactions of a particular type: k1 + k2 = k3 + k4 and ω(k1) + ω(k2) = ω(k3) + ω(k4). Generally, given a dispersion relation ω(k) with one or more branches, one needs to compute all lowest-order resonances for N = 3, N = 4, and so on, in order to describe nonlinear dynamics of resonant wave interactions with the normal-form analysis.
Time evolution of N resonant waves can be studied with an asymptotic multi-scale expansion method. In this method, a solution of the system u = u(x,t) is assumed to be close to a linear superposition of N resonant waves with slowly varying amplitudes. For instance, resonant interaction of three waves is described by the expansion:
u(x,t) = ε [a(εx,εt) exp(i (kx - ω(k)t)) + a1(εx,εt) exp(i (k1x - ω(k1)t)) + a2(εx,εt) exp(i (k2x - ω(k2)t))],where ε is small parameter and epsilon2-terms are not written. The evolution equations for the wave amplitudes take the form:
i (at + vax) = γ a1 a2 exp(-iΔt), i (a1t + v1a1x) = γ1 a a2* exp(iΔt), i (a2t + v2a2x) = γ2 a a1* exp(iΔt).Here Δ = ω(k)-ω(k1)-ω(k2) is the frequency detuning from the exact resonance; v, v1, v2 are group velocities of the three waves, and γ, γ1, γ2 are coupling coefficients in systems with quadratic nonlinearities. In nonlinear dispersive systems with conserved energy, parameters γ, γ1, γ2 are real.
Typical dynamics of the resonant three-wave interaction can be studied from the coupled-mode system for space-independent waves a(t), a1(t), a2(t) in the case of exact resonance, when Δ = 0. Without loss of generality, the real coupling coefficients can be normalized to be equal and positive: γ = γ1 = γ2 > 0. After these simplifications, the coupled-mode system has the following Manley-Rowe constants of motion:
|a|2 + |a1|2 = C1, |a|2 + |a2|2 = C2, |a1|2 - |a2|2 = C.The time evolution of wave amplitudes a(t), a1(t), a2(t) display two typical scenarios. If the wave with low frequency (ω1, ω2 < ω) is initially pumped into the system (e.g. either |a1|2 >> |a|2, |a2|2 or |a2|2 >> |a|2, |a1|2 at t = 0), then the other two resonant waves remain small throughout the whole time evolution. Indeed, it is seen from Manley-Rowe constants that when |a|2 grows, |a1|2 and |a2|2 decay. If either |a1|2 or |a2|2 were initially small, their decay (and the growth of |a|2) is limited by a small value of C1, C2 in the Manley-Rowe relations.
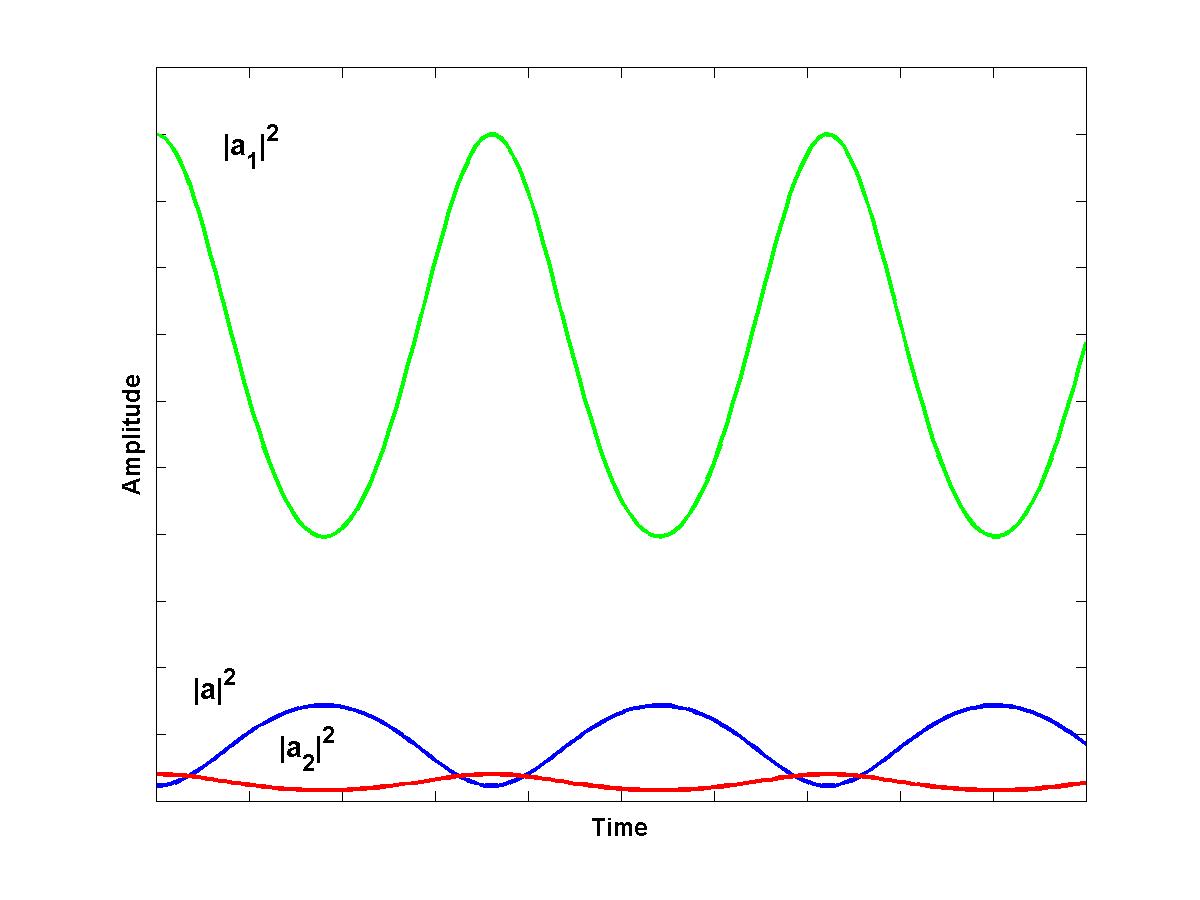
If however the wave of high frequency ω is initially pumped, then the waves of low frequencies ω1, ω2 may grow simulteneously. In this case, the resonant three-wave interactions display a sharp exchange of energy between the high-frequency wave and the two low-frequency waves. This process is referred to as the splitting or decaying instability of the high-frequency wave. As seen from the coupled-mode equations for small a1, a2, the amplitude a(t) does not change in time in the first-order approximation, while amplitudes a1(t), a2(t) grow exponentially as exp(|γ a| t). The high-frequency wave |a|2 decays into the two low-frequency waves |a1|2 and |a2|2, but the two waves merge back to the high-frequency wave later in the time evolution.

Resonant nonlinear three-wave interactions are known in many physical situations, such as in water waves, nonlinear optics, acoustics, and plasma physics. In nonlinear optics, resonant three-wave interactions are used in parametric amplifiers and oscillators, χ(2) optical materials, self-induced transparency, and stimulated Raman scattering. Four-wave mixing occur in optical communications and leads to growth of ghost pulses in an optical signal sequence. In water waves, resonant wave interactions explain effects of weak turbulence of gravity and gravity-capillary waves, as well as Rossby waves in atmosphere. In plasma physics, nonlinear dynamics of high-temperature plasmas in a magnetic fields involve wave-particle and wave-wave interactions. Resonant three-wave interactions occur in ionospheric propagation, plasma heating with high-power electromagnetic sources, microwave sources, and laser sources.
