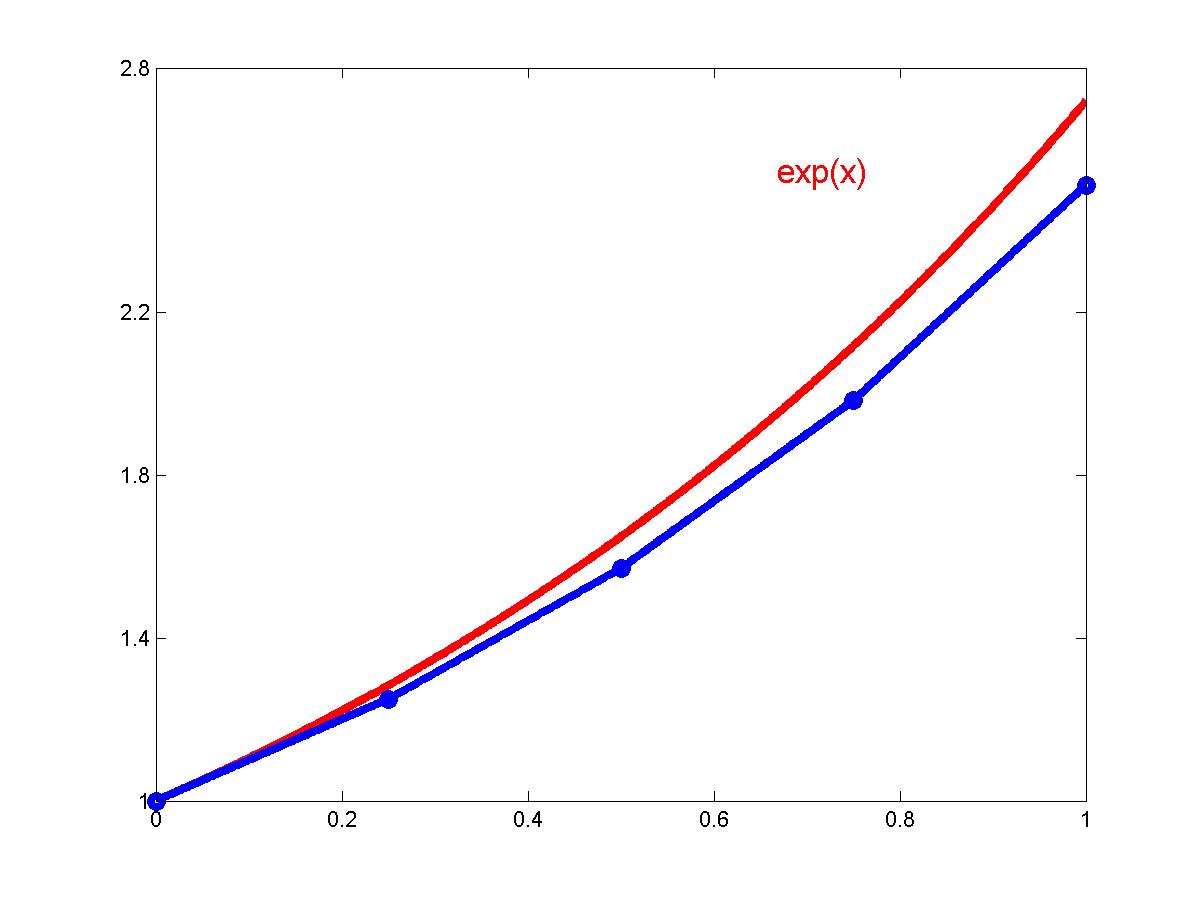
The function y = exp(x) solves the differential equation for exponential growth y' = y subject to the initial condition y(0) = 1. If the differential equation is solved numerically between 0 < x < 1, then the irrational number e = exp(1) can be approximated by the numerical solution at x = 1. One of the simplest ODE methods is the Euler's method which replaces the actual curve y = y(x) by its straight line piece-wise approximation with the same slope (click to enlarge the figure).

The numerical value for e is under-estimated due to this method. The numerical approximation is getting better by increasing the number of points at the interval between x = 0 and x = 1.
|
This demonstration uses the MATLAB function euler.m. |