Numerical differentiation is inherently ill-conditioned process. Two factors determine the error induced when the "exact" derivative I'(t0) is replaced by any of the difference approximations: truncation and round-off errors (see Lecture 1.2).
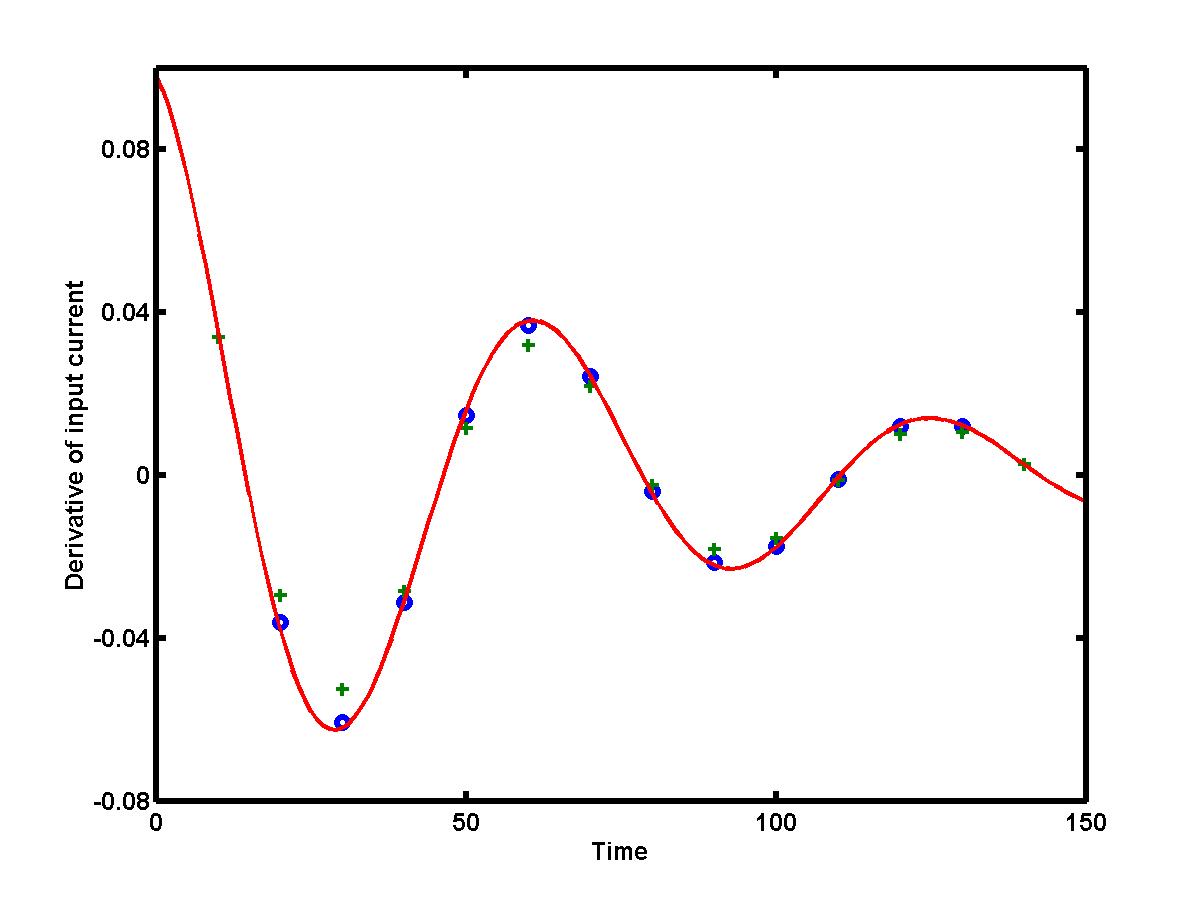
If the step size h between two adjacent values becomes smaller, the truncation error of the difference approximation decays. For example, if the step size is reduced by half, the truncation error of the central difference approximation is reduced by four. Therefore, if we can control the step size for data samples, then the truncation error can be reduced to any digit after the period! The figure below presents two central difference approximations for the derivative of the current I = I(t) (view the data values for the current). The approximations are obtained with step size h = 10 (green pluses) and with step size h = 5 (blue dots), versus the exact derivative I'(t) (red solid curve). The error of central difference approximation clearly reduces with smaller step size h.

However, the numerical approximation for the derivative could be really bad for smaller step sizes h. Indeed, when the step size is small, the central difference is taken for almost equal values I1 and I-1. Due to round-off error, it may lead to catastrophic cancellation and loss of accuracy in numerical computation. The smaller is the step size, the larger is the round-off error!
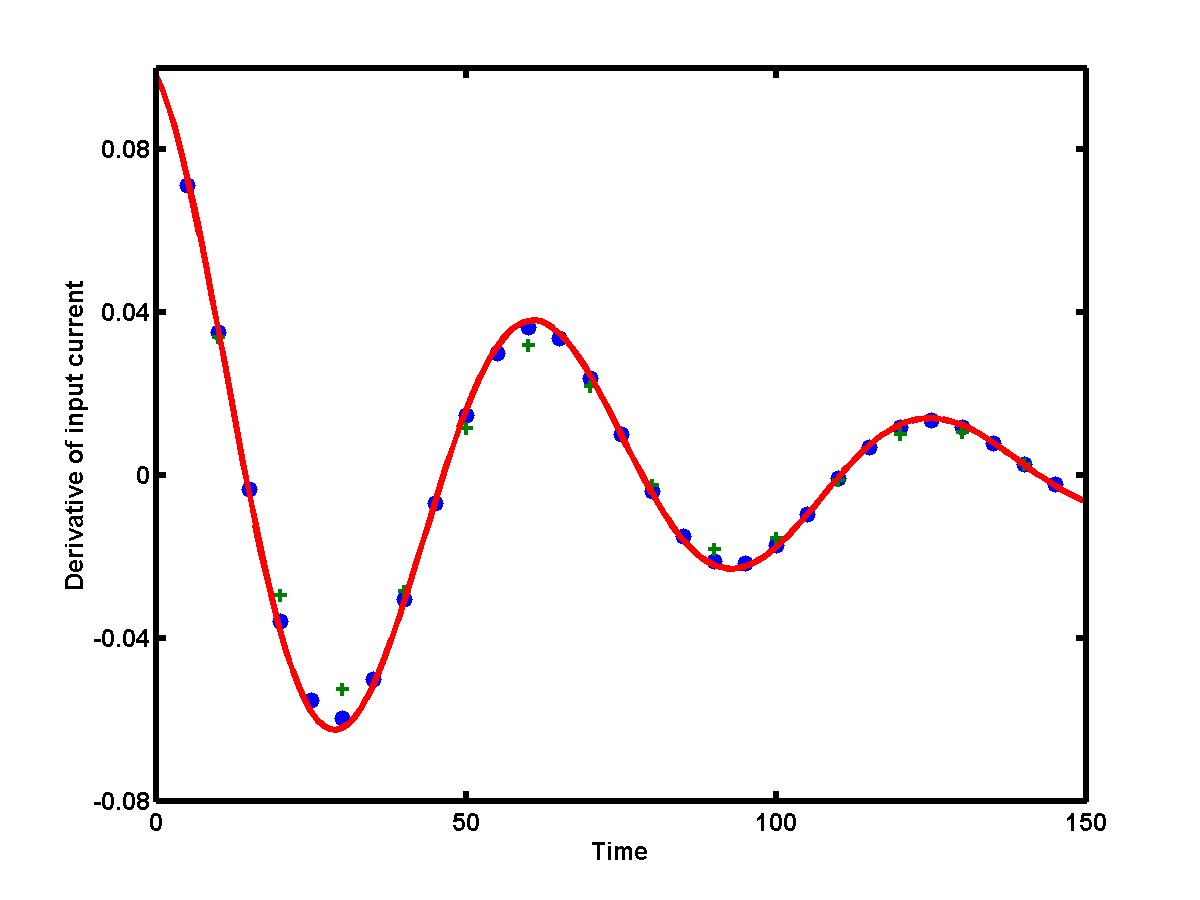
An optimal step size h exists when the sum of truncation and round-off errors are minimized (i.e. the optimal step size should be sufficiently small for small truncation errors and it should be sufficiently large for small round-off errors). However, the data samples are given in many cases with a fixed step size h that can not be controlled. If this is the case, the numerical approximation for derivative can be improved by including more points in the difference approximation. Two methods are used for finding multi-point difference approximations: one is based on the polynomial interpolation (see Lecture 3.2) and the other one is the Richardson extrapolation (see Lecture 3.3). The figure below presents the central difference approximations for the derivative of the current I = I(t) with the step size h = 10: blue circles are found by five-point central differences, green pluses are obtained by three-point central differences, and the exact derivative I'(t) is shown by red solid curve. Five-point difference approximation is clearly more accurate than the three-point difference.