| Mathematical Modeling | PDE Theory | Spectral Theory | Evolution Equations |
|---|
Waves are typically associated with perturbations that propagate in a system and transfer the energy of the system. Wave dynamics is possible both in conservative and dissipative (active) systems. Physical models of nonlinear waves are derived to simplify a complicated system of primary equations in a number of approximations. The same equations at the leading order describe main effects such as nonlinearity, dispersion, diffraction, diffusion, damping and driven forces, and resonances that determine wave propagation. Wave models are divided into several classes of fundamental nonlinear evolution equations such as kink-antikink (sine-Gordon), long-wave (Kortewed--Vries and Boussinesq), envelope-wave (nonlinear Schrodinger), and nerve-pulse (Fitz-Hugh--Nagumo) equations.

In conservative systems, wave dynamics of small amplitudes occurs typically in a neighboroughood of local minima of potential energy. A system of nonlinear massive pendulums represents a mechanical model for wave propagation. The pendulums swing on a rigid rod under the gravity force and couple each other with elastic springs. Wave oscillations in this mechanical system is described in a continuum approximation by the sine--Gordon equation, where φ is the angle between a pendulum and the vertical axis.
φtt - φxx + sin φ = 0.Surface water waves in oceans, seas and lakes represent another class of wave phenomena. Tsunami wave is an example of a nonlinear wave, that arises after underwater earthquakes or underwater volcano eruptions and may reach heights in 20-30 meters. Since tsunami waves are as long as tens and hundreds kilometers, the ocean can be considered as shallow for such waves. The shallow water approximation results in the Boussinesq system:
ut + u ux + ηx - utxx = 0, ηt + ux + η ux + u ηx = 0where η is the wave surface elevation and u is the horizontal velocity. The Boussinesq system in a linear approximation takes the form of the wave equation: ηtt - ηxx = 0. The wave equation has a general solution in the form of two waves: η = f(x-t) + g(x+t). When the waves are separated in space, small nonlinearity and dispersion are captured in the unidirectional approximation in the Korteweg-de Vries (KdV) equation:
ηt + ( 1 + 1.5 η ) ηx + 0.5 ηxxx = 0.The KdV equation was derived in 1895 as a model that explains the phenomenon of steady-state propagation of a solitary wave discovered by J. Russell in 1834. Solitary waves of the KdV equation are now referred to as solitons and their remarkable properties were studied in great details in the late 20th century.
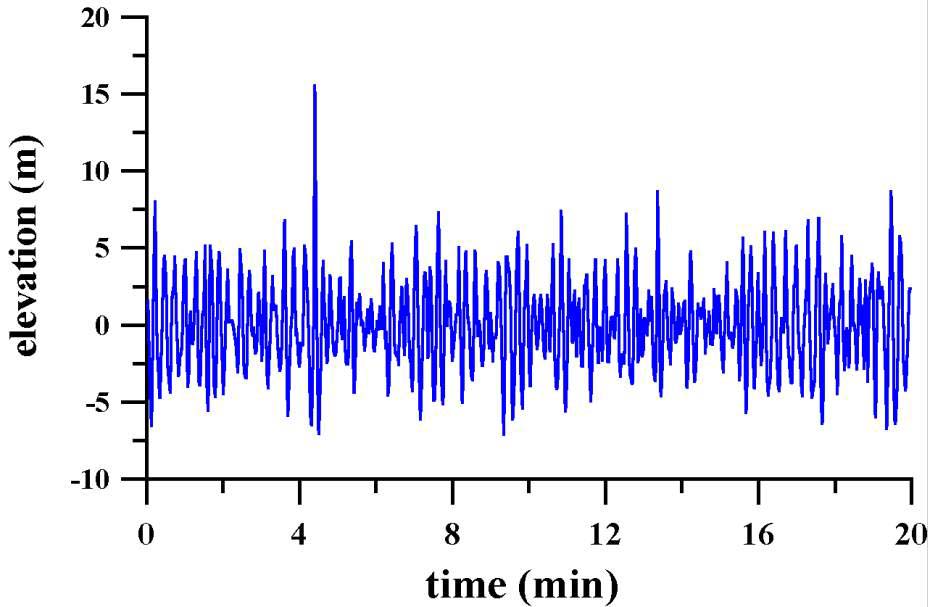
Oceanic waves generated by wind can reach anomalous high amplitudes in 10-20 meters. Such giant surface waves are called freak or rogue waves. They are formed as a result of a nonlinear interaction of multiple spectral components of the wave perturbations that propagate with different group velocities. The physical model for freak waves is based in the weak amplitude approximation on the nonlinear Schrodinger (NLS) equation:
i ψt + α ψxx + γ |ψ|2 ψ = 0,where ψ is the envelope amplitude of a wave packet centered in a spectral space at a wavenumber k0. Depending on the dispersion coefficient α and the nonlinearity coefficient γ, wave perturbations are focused or defocused in the time evolution of the NLS equation.
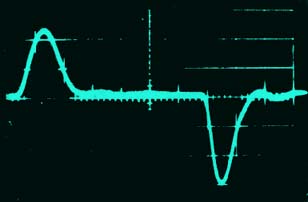
Another example of nonlinear waves includes nerve pulses and dissipative structures in reaction-diffusion systems. Physical models for nerve fibers are based on a system of coupled activator-inhibitor pairs, such as the Fitz-Hugh--Nagumo equations:
ut = Du uxx + f(u,v), vt = Dv vxx + g(u,v),where f(u,v) and g(u,v) are nonlinear functions. The reaction-diffusion systems exhibit static, travelling and pulsating structures that are relevant for modelling of brain activity.
|
|

|
Nonlinear Waves in Two Space Dimensions | |

|
Nonlinear Evolution Equations in Fluid Dynamics | ||

|
Neural Networks and Self-Organized Structures |